|
|
 Schrodinger cat animated on a quantum computer
Schrodinger cat animated on a quantum computer
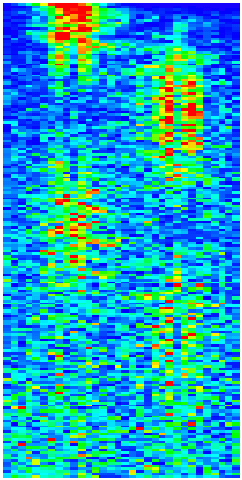
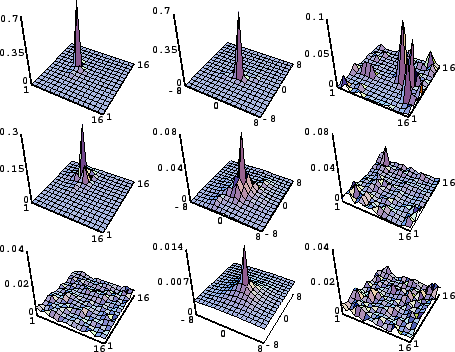
Time evolution of the Schrodinger cat:
probability distribution W(x) at -3.14 < x < 3.14 is shown
for different number of map iterations t, changing along y-axis
from t=0 (top) to t=180 (bottom).
Here for the double well map K=0.04, a=1.6 and
hbar = 4 x 3.1415/N with N=32. Quantum computation is done
with 6 qubits and and noisy gates of noise strength eps = 0.02,
and 2090 gates per one map iteration.
At t=0 initial coherent packet is located at x=-a.
From Ref. 131
http://xxx.lanl.gov/abs/quant-ph/0202113
|
|
|
|
 Quantum
fractal survivor Quantum
fractal survivor
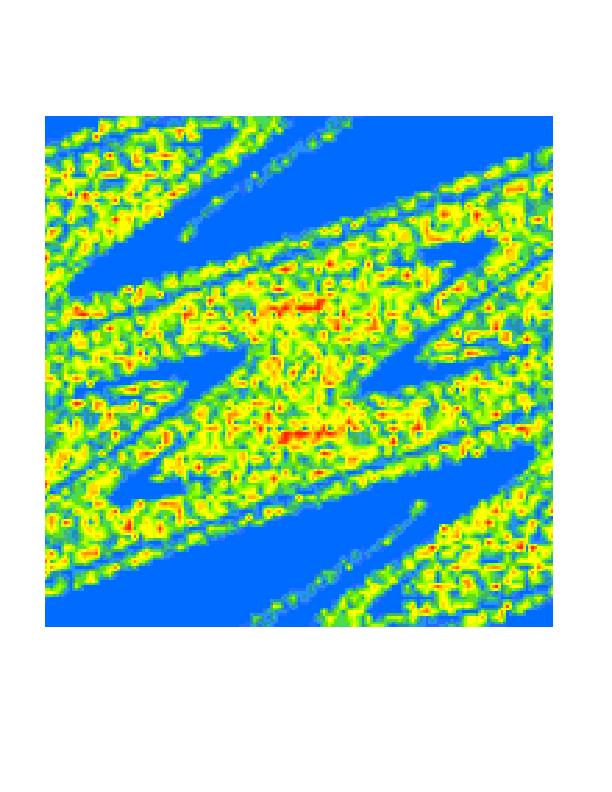
Quantum fractal eigenstate (Husimi function)
with minimal decay rate in the open
quantum kicked rotator with the chaos parameter K=7;
probability is absorbed outside of box size N=59049,
kick strength k=N/4.
From Ref. 97 (Physica D 131 (1999) 311)
http://xxx.lanl.gov/abs/cond-mat/9710118
|
|
|
|
|
 Quantum
chaos & quantum computers Quantum
chaos & quantum computers
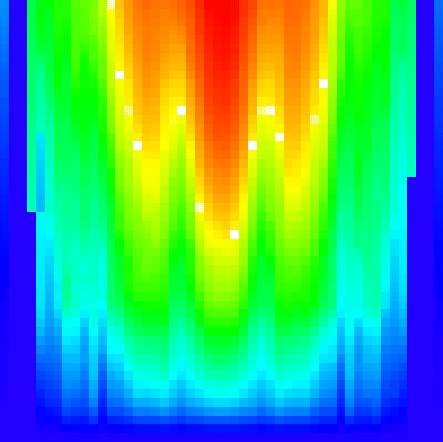
Quantum computer melting induced by the
coupling between qubits. Color represents the level of
quantum eigenstate entropy Sq
(blue - minimal Sq=0, red - maximal Sq=11)
for 12 qubits. Vertical axis gives the coupling
strength, horizontal one gives the energy of
computer eigenstate.
From Ref. 107 (1999)
http://xxx.lanl.gov/abs/quant-ph/9909074
|
|
|
|
|
|
|
|
 Delocalization of
two-particle ring Delocalization of
two-particle ring
near the Fermi level of 2d Anderson model
Probability distributions f and f_d for TIP in 2d disordered
lattice of size L=40, and interaction of radius R=12 and
width dR = 1. Left column, one-particle probability f
for W=8V: ground state at U=0 (top); ground state with binding
energy E = -1.05 V at U=-2V (middle); coupled state with
E = -0.19 V at U=-2V (bottom). Right column:
f for coupled state, compare to bottom left, at W=12V
and U=-2V with E = -0.19 V(top); inter-particle
distance probability f_d related to the middle left case (middle);
f_d related to the bottom left case (bottom). All data are
shown for the same disorder realisation.
From Ref. 110 (2000)
http://xxx.lanl.gov/abs/cond-mat/0002296
|
|
|
|
|
 Generalized
Cooper problem in the vicinity of Anderson transition Generalized
Cooper problem in the vicinity of Anderson transition
Probability distributions for two interacting particles
in the 3d Anderson model at the ground state. Probability
is projected on (x,y)-plane: one particle probability f_p
for Hubbard interaction U=-4 V (left column),
interparticle distance probability f_pd for U=-4 V (centrum
column), f_p for U=0 (right column); the disorder strength is
W/W_c=1.1 (upper line), W/W_c=0.5 (middle line), W/W_c=0.3
(bottom line); W_c=16.5 V is the critical disorder for
Anderson transition at half filling.
All data are given for the same realisation of disorder
for the system size L=16. Upper line corresponds to
the insulating noninteracting phase while two others are
in the metallic one at U=0.
From Ref. 109 (1999)
http://xxx.lanl.gov/abs/cond-mat/9911461
|
|
|
|
|
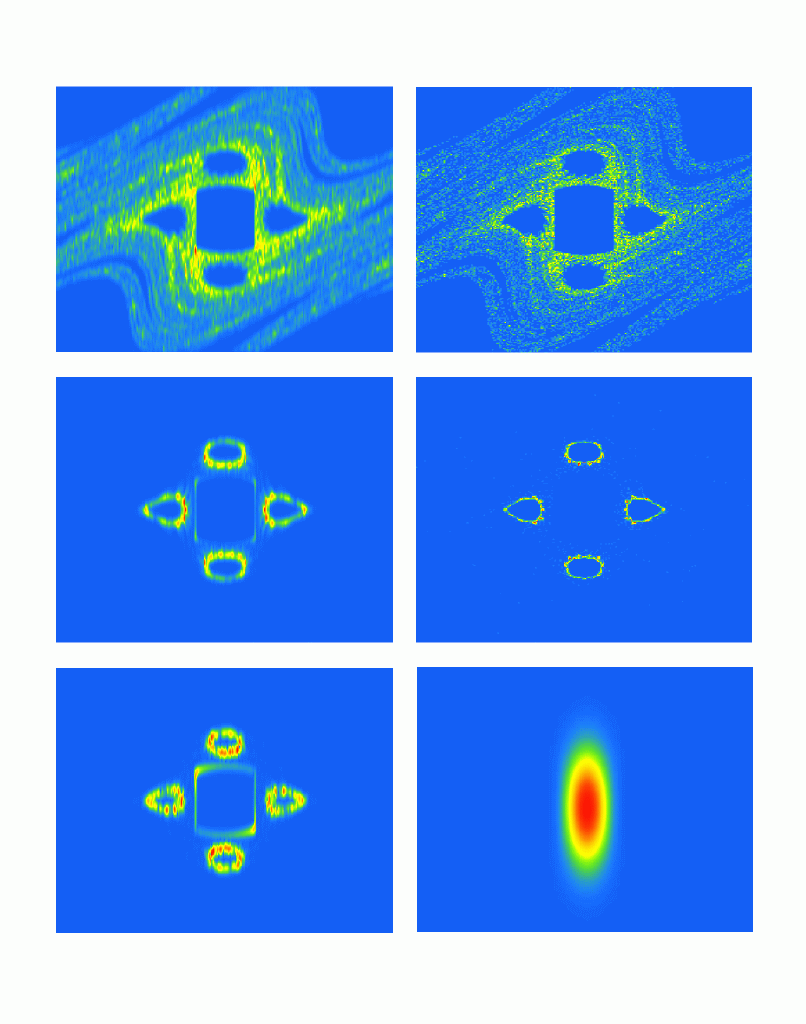
 Poincare recurrences: quantum and classical fractals Poincare recurrences: quantum and classical fractals
Quantum Husimi function in the kicked rotator
with absorption at time t=100 (top left);
5000 (middle left), 3x10^5 (bottom left);
right top (t=100) and middle (t=5000) are
classical probabilities,
number of levels N=3^8 , kick strength k=N/4,
chaos parameter K=7;
right bottom shows Husimi function
for N=3^6, t=10^7.
From Ref. 100 (Phys. Rev. Lett. 82 (1999) 524)
http://xxx.lanl.gov/cond-mat/abs/9807145
|
|
|
|
|
 Quantum
fractals in hydrogen atom Quantum
fractals in hydrogen atom
Probability distribution in action-phase
plane (y,x) for classical (left) and quantum (right)
atom in a microwave field after 50 microwave
periods, initial level n=1200.
From Ref. 108 (1999)
http://xxx.lanl.gov/abs/cond-mat/9911200
|
|
|
|
|
|
|
|
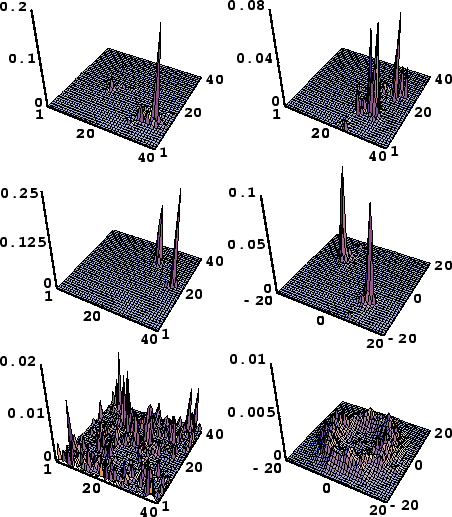
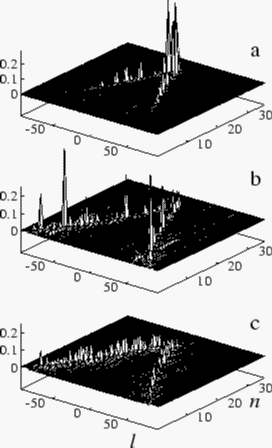
 Quantum ergodicity in rough billiards Quantum ergodicity in rough billiards
Transition from localization to Shnirelman ergodicity
on energy surface (n,l) for level number N =2250, l_max=95
and M=20; shown are the absolute amplitudes
of one eigenstate: a) localization for D=20,
b) Wigner ergodicity for D=80 and
c) Shnirelman ergodicity for D=1000.
From Ref. 92 (Phys. Rev. Lett. 79 (1997) 1833)
http://xxx.lanl.gov/abs/cond-mat/9807145
|
|
| |


 Quantum Gibbs distribution from dynamical thermalization
in classical nonlinear lattices
(video abstract 4mins)
Quantum Gibbs distribution from dynamical thermalization
in classical nonlinear lattices
(video abstract 4mins) 
Schrodinger cat animated on a quantum computer

Quantum fractal survivor

Quantum chaos & quantum computers
Dynamical turbulent flow on the Galton board with friction (video)

Delocalization of two-particle ring

Generalized Cooper problem in the vicinity of Anderson transition

Poincare recurrences: quantum and classical fractals

Quantum fractals in hydrogen atom


Quantum ergodicity in rough billiards