 |
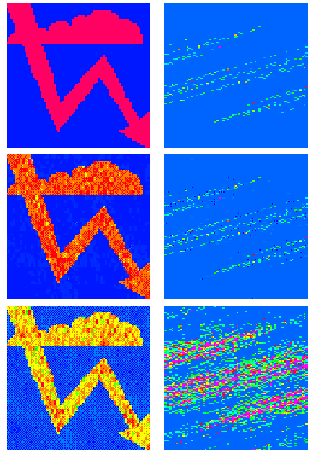
Strange attractor simulated on a quantum computer
Top: exact classical/quantum computation of the discretized dissipative map;
initial image (left) converged to the strange attractor after t=10 iterations (right).
Middle: quantum computation with noise amplitude eps=0.05 in each gate operation;
attractor at t=10 (right) and initial image recovered after 10 backwards iterations
with fidelity f=0.63 (left). Bottom: same as middle with eps=0.1 and f=0.15.
Left shows the central cell (-0.5< x,y <0.5), right shows the whole phase space.
Color marks the probability density (integrated over third and fourth registers),
from blue (density less than 1e-5) to red (maximal value). Here n_q=6, with in
total 28 qubits used.
From Ref. 13 (2002)
http://xxx.lanl.gov/abs/quant-ph/0203062 |
|
 |
Schrodinger cat animated on a quantum computer
Time evolution of the Schrodinger cat: probability distribution W(x) at
-3.14 < x < 3.14 is shown for different number of map iterations t, changing
along y-axis from t=0 (top) to t=180 (bottom). Here for the double well map
K=0.04, a=1.6 and hbar = 4 x 3.1415/N with N=32. Quantum computation is done
with 6 qubits and noisy gates of strength eps = 0.02, and 2090 gates per one
map iteration. At t=0 initial coherent packet is located at x=-a.
From Ref. 12 (2002)
http://xxx.lanl.gov/abs/quant-ph/0202113 |
|
 |
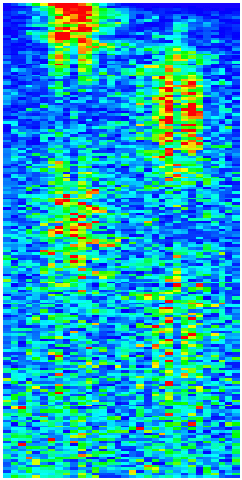
Efficient quantum computing of complex dynamics
Husimi function for the sawtooth map in action angle variables after 1000
kicks for 16 qubits and noisy gates with amplitude eps=0.0001.
From Ref. 10 (2001)
http://xxx.lanl.gov/abs/quant-ph/0107036 |
|
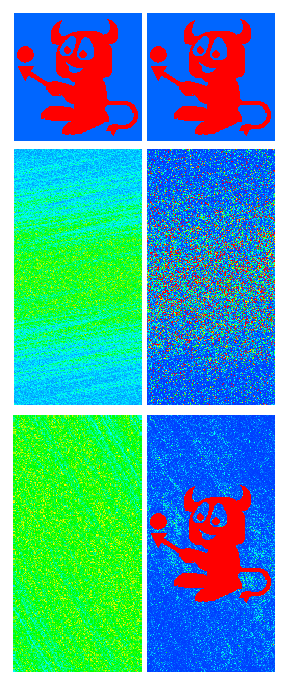 |
Quantum computer inverting time arrow for macroscopic systems
Evolution of a demon image through the Arnold cat map. Left column shows the
simulation on Pentium III, right column on Quantium I. Top: initial distribution
in the central cell (-0.5 < x,y < 0.5). Middle: distribution at t=t_r=35
in the whole phase space (-0.5 < x <0.5, -4< y <4).
Bottom: distribution at t=2t_r=70 in the two central cells ($-0.5 < x <0.5,
-1< y <1). The time-inversion is made at t_r=35, with accuracy E=1.e-8 for
Pentium III (error is done only at t_r), and with accuracy E=0.01 for Quantium I
(error is done at each gate operation). Color marks the density of particles/probability,
from blue (minimal) to red (maximal value). Here in total 26 qubits are used for
Quantium I; for Pentium III, 1.e+6 orbits are simulated.
From Ref. 9 (2001)
http://xxx.lanl.gov/abs/quant-ph/0105149 |
|
 |
Arnold-Shrodinger cat algorithm
Dynamics of Arnold-Schrodinger cat simulated on a classical (left) and quantum
computer (right), on a 128 X 128 lattice. Upper row: initial distribution;
second row: distributions after 10 iterations; third row: distributions
at t_2r=20, with time inversion made at t_r=10; bottom row: distributions
at t_2r=400, with time inversion made at t_r=200. Left: inversion is done
with classical error of one cell size (E=1/128) at t=t_r only; right: all
quantum gates operate with quantum errors of amplitude E =0.01; color from
blue to red gives the probability n_q=7, in total 20 qubits are used.
From Ref. 7 (2001)
http://xxx.lanl.gov/abs/quant-ph/0101004 |
|
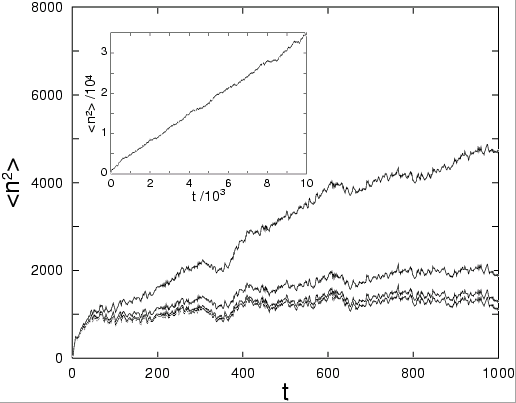 |
Quantum computing of kicked rotator
Dependence of the second moment n^2 on time t for different imperfection
strength E in quantum computing of kicked rotator for different number
of qubits n_q. Curves are for n_q=13, 12, 11 at E =0.0001 from top to bottom
and the lowest curve is for E=0 being the same for n_q=13, 12, 11. Here
k=10, K=5 and at t=0 all probability is at n=0. Inset shows the upper curve
up to larger times.
From Ref. 4 (2000)
http://xxx.lanl.gov/abs/quant-ph/0009005 |
|
 |
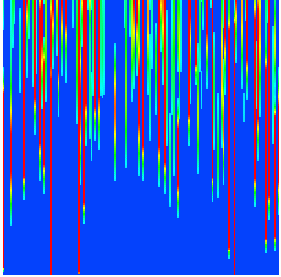
Quantum chaos in quantum computer core
Time explosion of quantum chaos in the quantum register: color represents
the value of the projection probability of an initial state on the quantum
register states ordered in energy, from red (maximal value) to blue (minimal
value). Horizontal axis corresponds to 150 states, the vertical axis to
150 time steps. A chosen initial state is the superposition of two quantum
register states. Here n=16 qubits are used with interqubit coupling above
(Fig. left) and below (Fig. right) the quantum chaos border.
From Ref. 2 (1999)
http://xxx.lanl.gov/abs/quant-ph/0005015 |
|
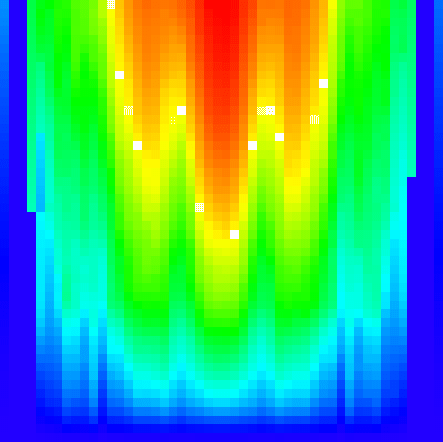 |
Quantum chaos & quantum computers
Quantum computer melting induced by the coupling between qubits. Color
represents the level of quantum eigenstate entropy Sq (blue - minimal Sq=0,
red - maximal Sq=11) for 12 qubits. Vertical axis gives the coupling strength,
horizontal one gives the energy of computer eigenstate.
From Ref. 1 (1999)
http://xxx.lanl.gov/abs/quant-ph/9909074 |
|








