Sputnik of Chaos

This special issue of Physica D represents selected proceedings of the Sputnik Conference of STATPHYS 20 ``Classical Chaos and its Quantum Manifestations'' organized in honor of Boris Chirikov, on the occasion of his 70th birthday on June 6th, and held in Toulouse, France on 16-18 July, 1998.

Sputnik is the name of the very first artificial satellite, launched back in 1957. In russian, this word means companion, but it is also a metaphor for a pioneering, outstanding achievement. These meanings seem appropriate for a portrait of Boris Chirikov. Back in 1959, he published a seminal article [1], where he introduced the very first physical criterion for the onset of chaotic motion in deterministic Hamiltonian systems. He then applied such criterion --now known as the Chirikov resonance-overlap criterion-- to explain puzzling experimental results on plasma confinement in magnetic bottles. As in an old oriental tale, Boris opened such a bottle, and freed the genie of Chaos, which spread the world over.

Boris Chirikov's research on chaos begun in a laboratory at the Kurchatov Institute for Atomic Energy (Moscow). In September 1959, he moved to Novosibirsk, at the Institute of Nuclear Physics founded by G. I. Budker, where he still continues to work. He became a correspondent member of the Russian Academy of Sciences in 1983, and a full member in 1992. (Further biographical details can be be found in [2].)

Giving a fair account of Chirikov's scientific output is an arduous task. Below we shall list ten prominent achievements of his, selected among those which are closer to the theme of this Conference, but we do so aware that much will be necessarily left out. What is more difficult to convey is a flavour of his personal qualities, his warmth and kindness, his attitude on life and science, and the influence these had on our scientific community. An event in his life paints some traits of his character: as a young researcher, he left Russia's capital city, the hectic rush for career and influence, and chose a simpler way of life, in a remote Siberian forest.

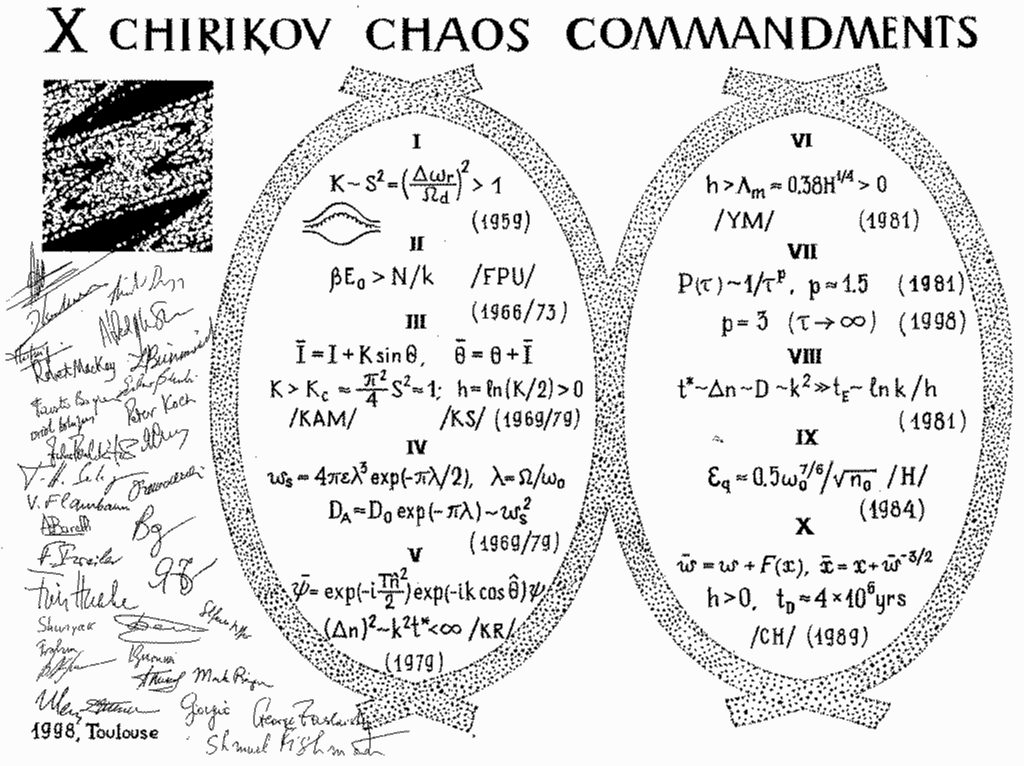
X Chirikov Chaos "Commandments"

I. The first rule represents the Chirikov resonance-overlap criterion introduced in [1] and then successfully applied to the determination of the confinement border for Rodionov experiments [3] with plasma in open mirror traps (the shape of magnetic lines is shown in the Figure). According to this criterion, a deterministic trajectory will begin to move between two nonlinear resonances in a chaotic and unpredictable manner, in the parameter range $K \sim S^2 >1$. Here $K$ is the perturbation parameter, while $S = \Delta\omega_r/\Omega_d$ is the resonance-overlap parameter, given by the ratio of the unperturbed resonance width in frequency $\Delta \omega_r$ (often computed in the pendulum approximation and proportional to the square-root of perturbation), and the frequency difference $\Omega_d$ between two unperturbed resonances. Since its introduction, the Chirikov criterion has become an important analytical tool for the determination of the chaos border [4]. The accuracy of the criterion can be improved on the basis of a renormalization approach to resonances on smaller and smaller scales [5]. For an up-to-date account of the status of particle confinement in magnetic traps, see [6,7,8].

II. This result [9] determines the energy border for strong chaos in the Fermi-Pasta-Ulam problem (FPU) [10], which became a cornerstone in modern statistical mechanics (see the historical review in [11]). The system represents a chain of $N$ weakly coupled nonlinear oscillators with the Hamiltonian $H={\sum_n} [p_n^2/2+(x_{n+1} - x_n)^2/2 + \beta (x_{n+1} - x_n)^4/4]$; initially only few long wave modes with wave vector $k$ and energy $E_0$ are excited. The chaos border is obtained from the Chirikov resonance-overlap criterion. New insights on this problem can be found in [12,13].

III. Here the first line represents the Chirikov standard map [14,15]. It is an area-preserving map with action variable $I$ and phase $\theta$. The bars denote the new values of the variables, while $K$ is the perturbation parameter. The dynamics becomes unbounded and diffusive in $I$ for $K > K_c \approx 1$, when all Kolmogorov-Arnold-Moser (KAM) invariant curves are destroyed. This value is obtained from the overlap criterion of first and higher order resonances [14,15]. For large $K > 4$ the Kolmogorov-Sinai (KS) entropy $h$, related to the exponential local instability of motion, is well-described by the given analytical formula. The Chirikov standard map provides a local description of the interaction between resonances, which finds applications in such diverse physical systems as particles in magnetic traps [15], accelerator physics [16], highly excited hydrogen atoms in a microwave field [17], mesoscopic resonance tunnelling diode in a tilted magnetic field [18]. Later, a refined analysis [19,20] gave the more precise value $K_c = 0.9716...$, related to the destruction of the KAM curve with the golden rotation number. For $K > K_c$ invariant curves are replaced by "cantori". Rigorous results were obtained in [21,22,23] (see also [24]). However, in spite of fundamental advances in ergodic theory [25], a rigorous proof of the existence of a set of positive measure of orbits with positive entropy is still missing, even for specific values of $K$.

IV. Here the first line represents the width $w_s$ of chaotic layer appearing around a separatrix of a nonlinear resonance [14,15]. This answers a question first addressed by Poincaré [27], who estimated the angle of separatrix splitting, but not the width of the layer. The above equation is written for the Hamiltonian $H(I,\theta,t) = H_0 + \epsilon \omega_0^2 \cos{\theta} \cos{\Omega t}$, where the unperturbed system is a pendulum with $H_0 = I^2/2 - \omega_0^2 \cos \theta$ and $w = H_0/\omega_0^2 - 1$ is the relative variation of the unperturbed pendulum energy. The second line describes the very slow rate of Arnold diffusion [26], a universally feature of such chaotic separatrix layers in systems with more than two degrees of freedom [14,28,15]. More recent results on chaos in separatrix layers and Arnold diffusion can be found in [29,30,31], see also the book [32].

V. Here the first equation describes the quantum kicked rotator, introduced [33], which is the quantized version of the Chirikov standard map (see III). The classical limit corresponds to $T \propto \hbar \rightarrow 0$, $k \propto 1/\hbar \rightarrow \infty$ and $K= k T = const$ with $I = T n$. The map gives the evolution of the wave function after one period of the perturbation ( $\hat{n} = -i \partial/ \partial \theta, \hbar =1$). The numerical results obtained in [33] showed that in the regime of strong chaos $(K \gg 1)$ the rotator energy, or the squared number of excited quantum levels $(\Delta n)^2$, grows diffusively in time as in the corresponding classical system, but only up to a break time $t^*$. After this time, the quantum energy excitation is suppressed while the classical one continues to diffuse. It was shown that $t^*$ grows with $k$, but an explanation of this phenomenon was found only later (see VIII).

VI. The result obtained in [34] showed that in general the dynamics of classical Yang-Mills fields is not completely integrable and can be chaotic. These studies were done for spatially homogeneous models of Yang-Mills fields introduced in [35], which can be described by an effective Hamiltonian with few degrees of freedom $N$. For a concrete case with $N=3$ it was found that the dynamics of color fields with energy $H$ is characterized by a maximal Lyapunov exponent $\Lambda_m \approx 0.38 H^{1/4} > 0$. As a result, the Kolmogorov-Sinai entropy $h$ is also positive, and the color field oscillations are chaotic. Later, low-energy chaos was also found for massive Yang-Mills fields [36].

VII. The results [37] showed that the statistics of Poincaré recurrences $P(\tau)$ in Hamiltonian systems with divided phase spaces decays as a power of time $\tau$ with the exponent $p \approx 1.5$. This algebraic decay originates from the long sticking of a trajectory near stability islands and the consequent slow diffusion on smaller and smaller scales of the phase space. This result also implies a slow decay of the correlation functions $C(\tau)$ related to recurrences as $C(\tau) \sim \tau P(\tau)$ [38,39,40]. The same exponent $p \approx 1.5$ was observed in other maps and Hamiltonian flows (e.g., the separatrix map, the Chirikov standard map etc.), up to times that are about $10^6$ times longer than an average return time [39,40,41]. For larger times the exponent reaches its asymptotic value $p=3$ [42] determined by the scaling properties of the diffusion rate near a critical KAM curve [38,41]. Since asymptotically $p>2$, the diffusion rate $D_c$ determined by such dynamics remains finite $(D_c \sim \int C(\tau) d \tau < \infty)$ .

VIII. In [43] it is shown that the break time $t^*$, at which the quantum suppression of classical chaos takes place, is proportional to the classical diffusion rate $D$. For the kicked rotator, this time scale determines also the number of excited unperturbed states $\Delta n \sim t^* \sim D \sim k^2 \propto 1/\hbar^2$. The time scale $t^*$ is much longer than the short Ehrenfest time $t_E$ on which a minimal coherent wave packet spreads over a large part of the phase space, due to the exponential local instability determined by the Kolmogorov-Sinai entropy $h$ [44,43]. The analogy between the quantum suppression of chaos and the Anderson localization in a disordered one-dimensional potential was established in [45]. In this sense the kicked rotator represents the first example of dynamical localization of chaos in a deterministic system without any randomness. The localization length is given by $l \sim \Delta n \sim D$. Recently the dynamical localization in kicked rotator was observed in the experiments with cold atoms in a laser field [46]. More details on the kicked rotator can be find in [47,48].

IX. On the basis of the results obtained for the kicked rotator (see V, VIII) the dynamical localization length was found for highly excited hydrogen atoms in a microwave field, that afforded a determination of the quantum delocalization border $\epsilon_q$ above which $(\epsilon_0 > \epsilon_q$) ionization takes place [49]. Here the microwave field strength $\epsilon$ and frequency $\omega$ are measured in rescaled atomic units so that $\epsilon_0 = \epsilon n_0^4, \;\; \omega_0 =\omega n_0^3$, where $n_0$ is the principal quantum number. For $\omega_0 > 1$ the border $\epsilon_q$ can be larger than the classical chaos border $\epsilon_c = 1/49 \omega_0^{1/3}$ [50]. As a result, for $\epsilon_q > \epsilon_0 > \epsilon_c$ the classical atom is completely ionized while the quantum is not. Moreover, if in the experiment the frequency $\omega = const$, then the quantum border grows with the level number $n_0$. This behavior, predicted in [49], was observed in laboratory experiments with hydrogen and Rydberg atoms [51,52,53]. As shown in [17], the dynamical localization for hydrogen atoms in a microwave field can be locally described by the kicked rotator. More details about quantum chaos in the microwave ionization of atoms can be found in [54,17,55].

X. This result [56] shows that the dynamics of the Halley comet can be modelled by a simple map (see the Figure): the comet energy change $(\bar{w} - w)/2$ is a periodic function of perihelion passage time $x$, measured in periods of Jupiter (first equation); the successive passage time $\bar{x}$ is given by the Kepler law (second equation) [in principle, Saturn also influences the comet's motion [56]]. This map is approximate but it describes the comet dynamics with very high accuracy [56]. Studies of this map showed that the Halley comet moves chaotically (the KS entropy is positive), and that the time of its diffusive escape from the solar system (both forward and backward in time) is rather short $t_D \approx 4 \times 10^6 years$. All this information was obtained from only 46 numbers, the perihelion passage times, found by extensive numerical simulations of other groups and astronomy observations found in historical records.

* * * * * * * * * *

These Chirikov Chaos "Commandments"$^*$, as well as his other results (e.g. [57,58,59]), are directly related to the modern physical developments of chaos presented at the Conference.

This Conference attracted more than one hundred participants. The majority were young researchers from all over the world, showing that this branch of science continues to generate enormous interest. The Conference logo, representing an eigenstate of the kicked rotator (see [60] for details), was chosen to emphasize the beauty and complexity of chaotic behavior. The following topics were in the center of discussions of participants:

Nonlinear systems and classical chaos. This topic was mainly addressed on the first day of the Conference. The problem of interaction of nonlinear resonances and their overlap in maps with quadratic nonlinearity was discussed by Chirikov and Lichtenberg (related to I, III). The properties of transport in quasi-periodic media were discussed by Sinai. The recent mathematical results for discrete breathers in nonlinear lattices were presented by Aubry and MacKay. The problems of space-time chaos, chaotic patterns and dynamical phase transitions in extended dynamical systems were analyzed by Bunimovich, Pikovsky and Ruffo (partially related to II). The properties of chaos borders and the statistics of Poincaré recurrences in area-preserving maps were discussed by Laskar, Artuso and Zaslavsky (see also III, IV, VII). The special role of symmetric periodic orbits and chaotic dynamics of classical wave fields were discussed by Seligman and Guarneri. The chaotic properties of billiards were analyzed by Bunimovich and Mantica. The problem of hamiltonian round-off errors and discretization in dynamical systems was highlighted by Vivaldi.

Spectrum, eigenstate properties, quantum ergodicity and localization. This topic was represented by investigations of a variety of models. Multifractal properties in models of quantum chaos and their relation to wave packet spreading were addressed by Geisel and Guarneri. The problem of emergence of quantum ergodicity in billiards was discussed by Borgonovi, Casati, Frahm, Prange, Prosen, and Ree. Fractal conductance fluctuations in billiards were studied by Ketzmerick. The localization of eigenstates in dynamical models and band random matrices was studied by Fishman, and Izrailev (related to V, VIII). The appearance of deviations from the random matrix theory and intermediate level statistics was discussed by Bogomolny. Quantum chaos in open systems, non-hermitian matrices and chaotic scattering was addressed by Casati, Maspero, and Fyodorov. The results of these studies found their applications in experiments with multimode optical fibers as discussed by Doya, Legrand, and Mortessagne. The theory of wave-chaotic optical resonators was developed and applied to droplet lasing experiments by Stone.

Periodic orbits and quantum chaos. New results on periodic-orbit theory for dissipative quantum dynamics were presented by Haake. Periodic orbits and their signatures in tunnelling, diffusion and scars were discussed by Creagh, Tanner and Borondo. Manifestations of periodic orbit quantization in such mesoscopic systems as a resonance tunneling diode in a tilted magnetic field were highlighted by Stone.

Quantum chaos in atomic physics. An experimental study of dynamical localization in the kicked rotator realized with ultra-cold cesium atoms in a laser field was presented by Raizen, who also discussed the effects of noise (related to V, VIII). Experimental investigations of quantum resonances in hydrogen atoms in a microwave field and effects beyond one dimension were presented by Koch (related to I, IX). A theory of microwave excitation of chaotic Rydberg atoms in a magnetic (or static electric) field, where more then 1000 photons are required to ionize one atom, was presented by Benenti (see IX). The chaotic dynamics of quasiparticles in trapped Bose condensates was studied by Fliesser and Graham. Properties of stable two electron configurations in strongly driven helium were discussed by Buchleitner. The statistical theory of dynamical thermalization and quantum chaos in complex atoms was presented by Flambaum (related to [59]). A theory of line broadering in recent experiments with a gas of interacting cold Rydberg atoms was developed by Akulin.

Quantum chaos in many-body systems. This is a relatively recent topic in the field of quantum chaos. New results for various systems were presented. The statistics of energy fluctuations of non-interacting fermions was discussed by Bohigas. Effects of interaction in finite Fermi systems were analyzed by Flambaum. Georgeot presented the conditions for applicability of random matrix theory to quantum spin glass clusters. The problem of two interacting particles propagating in a random potential was investigated numerically by Diaz-Sanchez. A transition from integrable to ergodic dynamics in many-body systems was investigated by Prosen. A review on quantum chaos in QCD vacuum was given by Shuryak.

The Conference demonstrated how varied are the physical applications of the ideas of classical and quantum chaos, ranging from QCD [61], cold [46], Rydberg [51] and complex [62] atoms to mesoscopic physics and chaotic light in droplets and microdisk lasers [63]. The achievments of physicists are complementary to the impressive mathematical developments of many twentieth-century mathematicians which are part of the legacy of Henri Poincaré, who discovered the first manifestations of what is now called deterministic chaos. Further mathematical results in this area can be found in the parallel special issue of the Annales de l'Institut Henri Poincaré on ``Classical and Quantum Chaos'', also dedicated to Boris Chirikov on the occasion of his 70th birthday [64].

In closing, we would like to thank the Conference sponsors, who helped to make this event possible: CNRS, Université Paul Sabatier, Institut Universitaire de France, IRSAMC, Région Midi-Pyrénées. We owe special thanks to Physica D, the journal where Boris Chirikov and his friend Joe Ford collaborated during many years. Our warmest thanks go to Sylvia Scaldaferro and Robert Fleckinger, for their day-by-day assistance in the organization; we also thank Armelle Barelli, Klaus Frahm and Bertrand Georgeot. We are thankful to F.M.Izrailev, V.V.Vecheslavov and F.Vivaldi for their friendly remarks we used here. Finally, we express our gratitude to the invited speakers and to the authors of the contributions to this volume, who enthusiastically accepted the invitation to participate.

J. Bellissard, O. Bohigas, G. Casati and D. L. Shepelyansky

Toulouse, 21 September, 1998